Is "Dollar Cost Averaging" a Bad Idea?
It's sometimes useful to run experiments yourself, isn't it?
New investors are often told that, when investing for the long term rather than chasing individual stocks, it is better to be invested for the longest possible time rather than trying to do "dollar cost averaging". DCA is the process of spreading out over time the purchasing of your investments. That way, you don't lose it all if the market drops the day after you invest.
Let me explain...
Imagine that it is 1994 and your rich uncle, Scrooge McDuck, has decided to gift you $1,200 per year. How generous!
He has stipulated that you must invest it in the S&P 500 - that's the top 500 companies in the world0.
He gives you two choices:
- Put $1,200 in on the 1st of January every year.
- Put $100 in on the 1st of the month every year.
How much money do you make in each scenario?
Get The Data
Kaggle has a download for the historic S&P 500 data. It goes from 1993 to 2024.
The data looks like this:
| Date | Open | High | Low | Close | Volume | Day | Weekday | Week | Month | Year |
|---|---|---|---|---|---|---|---|---|---|---|
| 29/01/93 | 24.70 | 24.70 | 24.58 | 24.68 | 1003200 | 29 | 4 | 4 | 1 | 1993 |
| 01/02/93 | 24.70 | 24.86 | 24.70 | 24.86 | 480500 | 1 | 0 | 5 | 2 | 1993 |
| 02/02/93 | 24.84 | 24.93 | 24.79 | 24.91 | 201300 | 2 | 1 | 5 | 2 | 1993 |
| 03/02/93 | 24.95 | 25.19 | 24.93 | 25.18 | 529400 | 3 | 2 | 5 | 2 | 1993 |
Experiment 1 - Time In The Market
Here's the algorithm we want to run.
- Start in 1994
- Set the investment as 1200
- Get the Opening price of the first entry of the year
- Get the Closing price of the last entry of the year
- Calculate the percentage difference
- Multiply the investment by the growth / fall
- Add 1200 to the investment
- Repeat from (3) for the next year.
Here's the code. I've made some assumptions - for example there are no trading fees, you buy at the opening price, and fractional dollars disappear. I'm aware this doesn't track perfectly but it isn't intended to; this is a rough and ready reckoner.
Open for Python Code
Python 3
import numpy as np
import locale
# Set for American currency
locale.setlocale( locale.LC_ALL, 'en_US.UTF-8' )
# Location of the data
file_path = 'data.csv'
# Load CSV into a NumPy array
data = np.genfromtxt(file_path, delimiter=',', names=True, dtype=None, encoding='utf-8')
# Count the number of unique years
unique_years = 0
# Total investment
total_investment = 0
# Yearly investment
yearly_cash = 1200
# Start with an opening of 0
opening = 0
# Loop through the years
for year in range( 1994, 2024 ):
# Add our yearly amount
total_investment += yearly_cash
# Get data for the current year
data_year = data[data['Year'] == year]
# Opening Price
if ( 0 == opening ) :
opening = data_year['Open'][0]
# Closing Price
closing = data_year['Close'][-1]
# Percentage Change
change = ( closing - opening) / opening
movement = "✅ +" if change > 0 else "❌ -"
# Calculate change in investment
total_investment = int( (1 + change) * total_investment )
# Print the running total
print ( f"{movement}{abs(change*100):05.2f}% {year} Total investment is " + locale.currency( total_investment, grouping=True ) )
# Set the new opening price
opening = closing
# Increment the number of years seen
unique_years += 1
print ( f"After {unique_years} years you have invested {locale.currency( yearly_cash * unique_years , grouping=True )}" )
print ( f"Your total amount is {locale.currency( total_investment, grouping=True )}" )
It spits out:
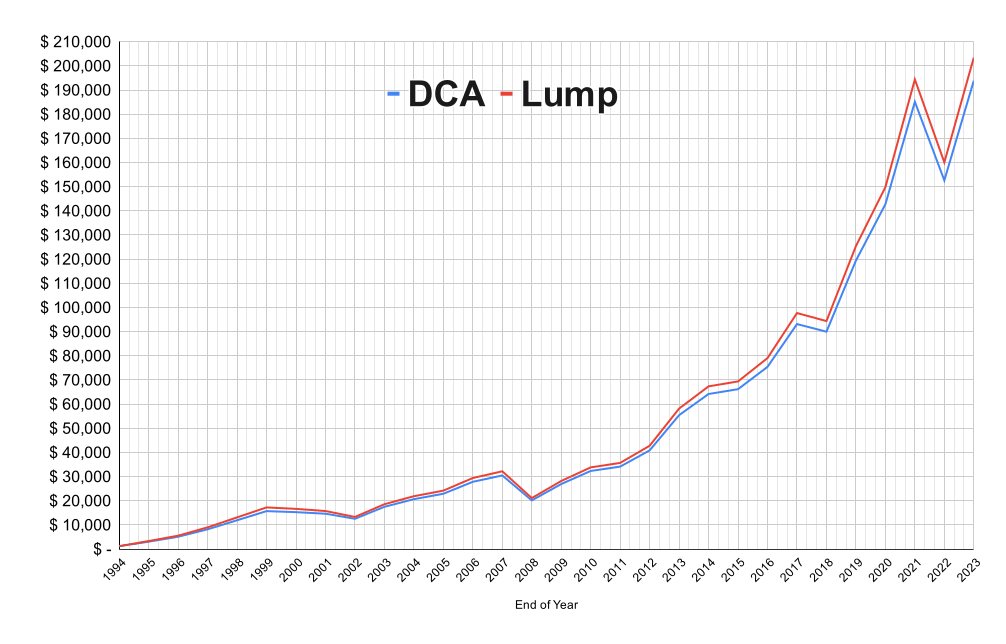
After 30 years you have invested $36,000 Your total amount is $203,445
Experiment 2 - Dollar Cost Averaging
OK! Can we beat that with DCA? In this scenario you take your uncle's money and invest 1/12th of it on the first trading day of every month.
Open for Python Code
Python 3
import numpy as np
import locale
# Set for American currency
locale.setlocale( locale.LC_ALL, 'en_US.UTF-8' )
# Location of the data
file_path = 'data.csv'
# Load CSV into a NumPy array
data = np.genfromtxt(file_path, delimiter=',', names=True, dtype=None, encoding='utf-8')
# Total investment
total_investment = 0
# Monthly investment
monthly_cash = 100
# Number of months run
number_of_months = 0
# Start with an opening of 0
opening = 0
# Loop through the years
for year in range( 1994, 2024 ):
# Get data for the current year
data_year = data[data['Year'] == year]
# There should be 12 months in every year, but let's double check!
unique_months = np.unique(data_year['Month'])
# Loop through the months
for month in unique_months:
# Add our monthly amount
total_investment += monthly_cash
# Filter data for the current month
data_month = data_year[data_year['Month'] == month]
# Opening Price
if ( 0 == opening ) :
opening = data_month['Open'][0]
# Closing Price
closing = data_month['Close'][-1]
# Percentage Change
change = ( closing - opening) / opening
movement = "✅ +" if change > 0 else "❌ -"
# Calculate change in investment
total_investment = int( (1 + change) * total_investment )
# Print the running monthly total
print ( f"{movement}{abs(change*100):05.2f}% {year}/{month:02.0f} Total investment is " + locale.currency( total_investment, grouping=True ) )
# Set the new opening price
opening = closing
# Increment the number of months
number_of_months += 1
# Yearly total
#print ( f"{movement}{abs(change*100):05.2f}% {year}/{month:02.0f} Total investment is " + locale.currency( total_investment, grouping=True ) )
print ( f"Your total amount is {locale.currency( total_investment, grouping=True )} after {number_of_months} months" )
The end result?
Your total amount is $193,891 after 360 months
That's $9,554 worse than shoving all the money in on January 1st.
Which... Look, $10k is $10k. I'd rather have it than not. But, in the context of these numbers, it doesn't feel significant. Does it?
Let's Graph It!
Conclusion
Dollar Cost Averaging is fine0. Over a long enough time you're probably marginally better off with lump-sum investing. But there's not much in it.
I'm sure you can construct scenarios where DCA is slightly preferential, and not every investment tracks the S&P500, and I'm sure my maths might be a little wonky, and obviously this is not financial advice. But, yeah, DCA if you want to; the difference in this example appears to be minimal.
@Edent The real question is, how can I find a rich relative and get them to give me money?
@Edent a somewhat fairer comparison would be dropping the the yearly lump in the middle of the year, else some of the difference is effectively the lost interest that you could have been earning on the cash even in a savings account. (Speaking as someone who spent many years working in the City on derivatives desks!)
Dinonerd says:
As I understand it, the big advantage of dollar cost averaging is that it reduces risk. In particular, you aren't going to invest (all) your money at a stock market peak, just before a crash.
Human nature makes that a bit more likely than if you picked a truly random date to invest a lump sum.
Also, FWIW, your examples are both DCA. The only difference is the frequency of investment.
Alex B says:
I just hacked the DCA simulator to embody the adage "Sell in May and go away".
If we just avoided buying between 1 May and 31 October each year, and invested $200 each month otherwise:
✅ +04.57% 2023/12 Total investment is $195,970.00 Your total amount is $195,970.00 after 360 months
So slightly better than naïve DCA.
If we liquidate our entire holdings in May, then put all those proceeds (+$200) back in the market in a lump sum in November:
✅ +04.57% 2023/12 Total investment is $119,153.00 Your total amount is $119,153.00 after 360 months
Oof!
If we take the proceeds, then use DCA to re-invest over the following 6 months from November:
✅ +04.57% 2023/12 Total investment is $24,470.00 Your total amount is $24,470.00 after 360 months
Double-Oof!
Ben Smith says:
I thought that the advocates of DCA recommended it in favour of holding investable cash and trying to time entry to 'the market'. I don't think I've ever seen it recommended to drip-feed money in per this comparison.
I am, however, also not a financial advisor.
More comments on Mastodon.